Contents

% Static and dynamic analysis for plane strain state
% 1. Mesh should be generated and exported by PDEtool  (Mesh --> Export Mesh)
% 2. Lines indicated by "<<<<<<<<" should be modified by user
% 3. Examples of PDEtool results postprocessing by "pdesmech" function
%    - mises=pdesmech(p,t,c,u,'tensor','von Mises', ...   % after: PDE   --> Export PDE &
%                     'application','pn','nu',0.3);       %        Solve --> Export Solution
%    - Sxx=pdesmech(p,t,c,u,'tensor','sxx')
format compact, '..........................................................................'

Data

E=210e9; nu=0.3; rho = 7800;       % <<<<<<<<  material parameters
mode=1;                            % <<<<<<<<  select the eigenmode to be presented
D = hooke(2,E,nu);

Determine number of nodes, elements and dof

[k,Nodes]=size(p);  % run pdetool first & execute: Mesh --> Export Mesh
[k,Nel]=size(t);
Ndof=2*Nodes;

Plot discretization

for iel=1:Nel
    nod1=t(1,iel); nod2=t(2,iel); nod3=t(3,iel);
    Edof(iel,1:7)=[iel,2*nod1-1,2*nod1,2*nod2-1,2*nod2,2*nod3-1,2*nod3];
    Ex(iel,1:3)=[p(1,nod1),p(1,nod2),p(1,nod3)];
    Ey(iel,1:3)=[p(2,nod1),p(2,nod2),p(2,nod3)];
end
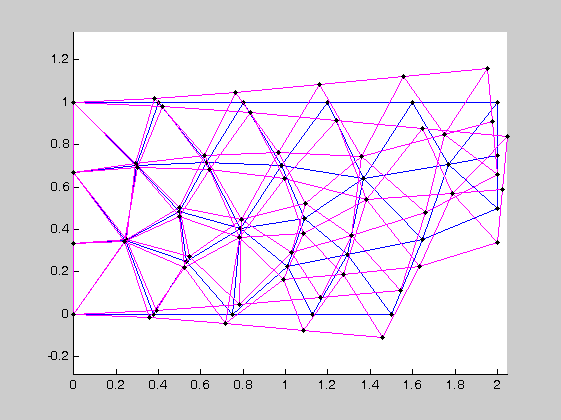
figure(1)  % elements
eldraw2(Ex,Ey,[1,4,1],Edof(:,1)), hold on, axis equal;

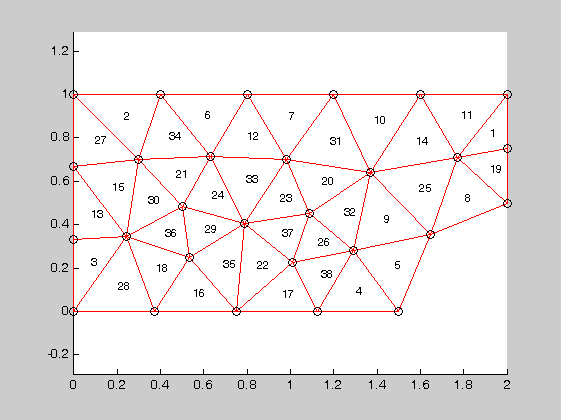
figure(2)  % nodes
eldraw2(Ex,Ey,[3,4,0]), hold on, axis equal;
for in=1:Nodes
    h=text(p(1,in),p(2,in),int2str(in));
    set(h,'fontsize',14,'fontweight','bold');
end

Account for boudary conditions

f=zeros(Ndof,1);         % global load vector - STATIC b.c.
f([14:2:20],1)=-20e6;  % <<<<<<<<
f([2,4],1)=-10e6;      % <<<<<<<<

kin_bc = ...              % <<<<<<<<  KINEMATIC b.c.
 [   1     0              % <<<<<<<<
     2     0              % <<<<<<<<
    23     0              % <<<<<<<<
    24     0              % <<<<<<<<
    21     0              % <<<<<<<<
    22     0              % <<<<<<<<
     5     0              % <<<<<<<<
     6     0 ];           % <<<<<<<<

Assemble stiffness matrix

KG=zeros(Ndof,Ndof);
for iel=1:Nel
    Kel=plante(Ex(iel,:),Ey(iel,:),[2 1],D);
    KG=assem(Edof(iel,:),KG,Kel);
end

Solve system of alg. equations

u=solveq(KG,f,kin_bc);

Plot deformed mesh

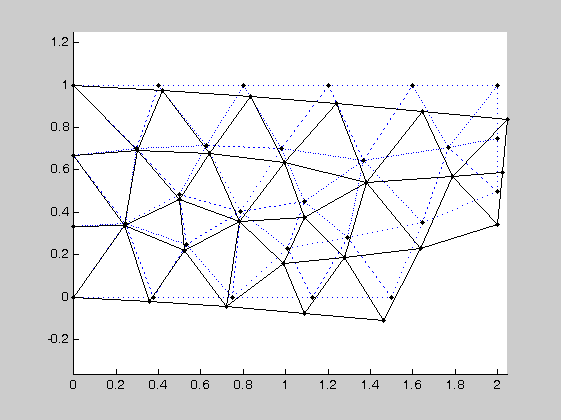
figure(3)
eldraw2(Ex,Ey,[3,2,0]), hold on, axis equal;
Ed = extract(Edof,u);
sfac=scalfact2(Ex,Ey,Ed,0.4);
eldisp2(Ex,Ey,Ed,[1,1,0],sfac); hold on;

Compute stresses

for iel=1:Nel
    Sig=plants(Ex(iel,:),Ey(iel,:),[2 1],D,Ed(iel,:));
    Smises(iel)=sqrt( 1/2*((Sig(1)-Sig(3)).^2 + (Sig(2)-Sig(3)).^2 + (Sig(1)-Sig(2)).^2+ ...
                            6*Sig(4).^2) );
end

Free vibrations

ML=zeros(Ndof,Ndof);   % lumped mass matrix
for iel=1:Nel
    Area=abs( (Ex(iel,1)-Ex(iel,3))*(Ey(iel,2)-Ey(iel,3)) - ...
              (Ex(iel,2)-Ex(iel,3))*(Ey(iel,1)-Ey(iel,3)) )/2;
    Mlum=eye(6)*Area/3*rho;
    ML=assem(Edof(iel,:),ML,Mlum);
end
[La,Egv]=eigen(KG,ML,kin_bc(:,1));

Plot selected eigen mode

figure(4)
eldraw2(Ex,Ey,[1,2,0]), hold on, axis equal;
U=Egv(:,mode);
Ed = extract(Edof,U);
sfac=scalfact2(Ex,Ey,Ed,0.4);
eldisp2(Ex,Ey,Ed,[1,3,0],sfac); hold on;
eldisp2(Ex,Ey,-Ed,[1,3,0],sfac); hold on;

Published with MATLAB® 7.6