Zanim przejdziemy do analizy nieliniowej i zbadamy np. rozwój stref plastycznych w materiale, musimy zawsze wykonać powyższą wstępną analizę liniową.
Celem obliczeń jest teraz opis deformacji próbki w zakresie plastycznym. Rozpocznijmy od uzupełnienia danych materiałowych niezbędnych w analizie sprężysto-plastycznej przy założeniu najprostszej teorii plastyczności Hubera-Misesa-Hencky'ego (H-M-H) ze wzmocnieniem izotropowym. W teorii tej powierzchnia plastyczności wyraża się wzorem:
w którym 
jest tensorem naprężeń, 
zastępczą miarą
odkształceń plastycznych (zwaną też parametrem wzmocnienia),
drugim niezmiennikiem tensora
naprężeń, zaś 
naprężeniem granicznym.
Definicja wynika z tzw. hipotezy wzmocnienia (por. np. [1]).
Funkcja 
odzwierciedla wzmocnienie lub osłabienie materiału.
Jest ono opisane przez tzw. moduł wzmocnienia:
który określa nachylenie wykresu zależności pomiędzy
naprężeniem granicznym a miarą odkształceń plastycznych.
W szczególności dla liniowego wzmocnienia (osłabienia) H jest stałą.
Początkowa wartość naprężenia granicznego jest granicą plastyczności
i oczywiście dla
mamy do czynienia z idealną plastycznością.
W naszym zadaniu dodatkowe dane materiałowe dla stopu
aluminium są następujące:
granica plastyczności 
i moduł wzmocnienia liniowego 
.
Uzupełniona tablica danych materiałowych w zbiorze
platehole.dat wygląda tak:
'MATERIALS'
1 YOUNG 70000.
POISON 0.2
YIELD VMISES
YLDVAL 243.
HARDEN WORK
HARDIA 243. 0.
1400. 0.5
W definicji materiału HARDEN WORK wybiera energetyczną hipotezę
wzmocnienia izotropowego (work hardening), a liczby po HARDIA
określają dwa punkty wykresu w przestrzeni ( 
)
definiującego przyjęty moduł wzmocnienia.
Musimy się teraz zastanowić nad liczbą i wielkością przyrostów obciążenia, które chcemy użyć w przyrostowo-iteracyjnym rozwiązaniu zadania nieliniowego algorytmem Newtona-Raphsona. Zazwyczaj w pierwszym przyroście chcemy się zbliżyć dużym krokiem do granicy plastyczności, pozostając jednak w zakresie sprężystym, zatem proces iteracyjny w tym kroku jest natychmiastowo zbieżny (równowaga sił zewnętrznych i wewnętrznych jest zachowana). Następnie wykonujemy kilkadziesiąt mniejszych kroków w zakresie nieliniowym, w których konieczne są już iteracje.
Komentarza wymaga zatem wielkość obciążenia lub kinematycznego
wymuszenia zadanego w zbiorze platehole.dat.
Takie obciążenie odniesienia (konfiguracyjne), które będziemy
stopniowo zwiększać, przyjmowane jest zazwyczaj jako jednostkowe,
chyba, że wygodniej nam zadać wielkości oszacowane w elementarnych
obliczeniach. W naszym zbiorze danych przyjęto w przypadku
DEFORM przemieszczenie górnego brzegu równe
, czyli
odpowiadające uplastycznieniu ćwiartki próbki bez otworu,
natomiast w przypadku NODAL siłę odpowiadającą
stałemu naprężeniu równemu granicy plastyczności na odcinku 5mm
wzdłuż osi x, tj. 
przy grubości próbki 1mm.
Uwagę skupimy na sterowaniu przemieszczeniem. Zauważmy, że
nasza próbka jest osłabiona otworem i uplastyczni się
znacznie wcześniej niż próbka bez otworu. Na rys. 5 możemy
odczytać, ze maksymalne naprężenie główne wywołane w zadaniu
liniowym obciążeniem
odniesienia wynosi 679 
, zatem już ok. 0.35 tego
obciążenia spowoduje osiągnięcie w elemencie nr 1 granicy
plastyczności .
Przyjmiemy zatem pierwszy krok 0.3, a następnie
jeszcze 7 kroków po 0.1 obciążenia (w tym wypadku deformacji)
odniesienia.
Przykładowy zbiór komend do analizy nieliowej, nazwany tu non.com, jest następujący:
*filos
initia ma=2000000 di=300
*input
echo
*elasse
store.x
*elmat
*loads
*order
*solve
*nonlin
initia
analys physic
use
plasti.t
end use
end initia
loading
load(1): (1) 1.0 /
end loading
select
nodes 165 187 198 209 220 231 232 242 /
elemen 1 /
: elemen none /
end elemen
end select
output tabula
displa total coor
force residu
strain total intpnt coor
stress total intpnt coor
end output
execute load(1) steps
size 0.3 0.1(7) /
perform newton regula mi=10
: perform.r newton regula mi=10
: norm energy contin co=0.000001
norm force contin co=0.000001
use
plasti.t
end use
end execut
*end
Zbiór ten rozpoczyna się od powtórzenia wstępnej analizy liniowej
(bez modułu *POST), choć jeśli to zadanie wykonujemy
bezpośrednio po zadaniu liniowym, czyli uaktywniając w skrypcie
run następną linię:
#!/usr/local/bin/tcsh cd $HOME/diana_directory # # diana $FFDIR/testjp.ff mesh.dat mesh.com # diana $FFDIR/testjp.ff platehole.dat lin.com diana $FFDIR/testjp.ff platehole.dat non.com # diana $FFDIR/testjp.ff graf.com # diana $FFDIR/testjp.ff post.comwówczas niezbędne informacje są już pamiętane z bazie danych $FFDIR/testjp.ff i komendy przed linią *nonlin można pominąć.
W module *nonlin żądamy najpierw inicjalizacji
analizy nieliniowej. Pomiędzy komendami initia
i end initia deklarujemy analizę fizycznie nieliniową
i użycie algorytmów plastyczności.
Następnie specyfikujemy obciążenie do przyrostowania. Linia
load(1): (1) 1.0 /
oznacza, że przypadek obciążenia nr 1 przeskalowany przez mnożnik 1.0
jest pierwszym obciążeniem konfiguracyjnym.
Kolejne słowo kluczowe select rozpoczyna deklarację
węzłów i elementów do wydruku, zaś po słowach output tabula
wybierane są wielkości
do wydruku
Po tych wstępnych deklaracjach uruchamiamy proces przyrostowy
komendą execute load(1) steps. Podajemy długości kroków
(liczba powtórzeń kroku w nawiasach)
size 0.3 0.1(7) /
typ algorytmu do wykonania
z maksymalną liczbą iteracji w ramach przyrostu
perform newton regula mi=10
normę zbieżności, np. dla sił residualnych
norm force contin co=0.000001
(contin oznacza żądanie kontynuacji przyrostow nawet
w wypadku nie osiągnięcia zbieżności w danym kroku).
Dodatkowo deklarujemy ponownie użycie procedur plastyczności.
Po wysłaniu zadania do kolejki możemy śledzić przebieg
zadania nieliniowego oglądając końcowe linie zbioru
diana.out komendą tail -f.
Najważniejsze fragmenty tego zbioru wyglądają tak:
1:*FILOS!!! Tutaj całe echo komend i danych !!!
/DIANA/EA/IT30 19:10:32 1.42-CPU 2.85-IO 796.-FA BEGIN
ELEMENT-TYPE DATA READY: HE= 50 NE= 50 MD= 16
!!! Tutaj przebieg wstępnej analizy liniowej !!!
/DIANA/NL/IN30 19:10:42 3.32-CPU 5.78-IO 1768.-FA BEGIN
ANALYSIS INCLUDES:
( QUALIFIERS AND PARAMETERS CAN BE OVERRULED PER EXECUTION BLOCK )
PHYSICALLY NONLINEAR BEHAVIOR:
PLASTI.T NS= 10 TY= 1.000E-04
/DIANA/NL/LO30 19:10:44 3.87-CPU 6.05-IO 1880.-FA BEGIN
/DIANA/NL/XQ31 19:10:45 3.92-CPU 6.23-IO 1937.-FA BEGIN
STEP 1 INITIATED:
LOAD INCREMENT: LOADING( 1) * 3.000E-01
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.16021D+05 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 0
STEP 1 : FORCE NORM = 5.367E+02 TOLERANCE = 1.000E-06
RELATIVE OUT OF BALANCE FORCE = 1.700E-14 CHECK = TRUE
STEP 1 TERMINATED, CONVERGENCE AFTER 0 ITERATIONS
TOTAL LOAD FACTOR: LOADING( 1) * 3.000E-01
/DIANA/PO/WR30 19:10:49 5.07-CPU 6.65-IO 2175.-FA BEGIN
TABULA file diana.tb OPENED
/DIANA/NL/XQ31 19:10:50 5.28-CPU 6.98-IO 2254.-FA BEGIN
STEP 2 INITIATED:
LOAD INCREMENT: LOADING( 1) * 1.000E-01
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.16021D+05 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 3
STEP 2 : FORCE NORM = 7.148E+02 TOLERANCE = 1.000E-06
RELATIVE OUT OF BALANCE FORCE = 7.804E-03 CHECK = FALSE
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.15767D+05 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 2
RELATIVE OUT OF BALANCE FORCE = 9.045E-04 CHECK = FALSE
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.15828D+05 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 2
RELATIVE OUT OF BALANCE FORCE = 4.906E-07 CHECK = TRUE
STEP 2 TERMINATED, CONVERGENCE AFTER 2 ITERATIONS
TOTAL LOAD FACTOR: LOADING( 1) * 4.000E-01
/DIANA/PO/WR30 19:10:57 8.15-CPU 7.45-IO 2778.-FA BEGIN
TABULA file diana.tb OPENED
!!! Tutaj przebieg przyrostów 3-7 !!!
/DIANA/NL/XQ31 19:11:51 29.87-CPU 12.07-IO 6706.-FA BEGIN
STEP 8 INITIATED:
LOAD INCREMENT: LOADING( 1) * 1.000E-01
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.88543D+04 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 67
STEP 8 : FORCE NORM = 1.365E+03 TOLERANCE = 1.000E-06
RELATIVE OUT OF BALANCE FORCE = 1.226E-02 CHECK = FALSE
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.69655D+04 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 67
RELATIVE OUT OF BALANCE FORCE = 5.056E-03 CHECK = FALSE
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.56447D+04 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 66
RELATIVE OUT OF BALANCE FORCE = 9.464E-04 CHECK = FALSE
DECOMPOSITION SIMULATED: MB= 54 NQ= 333 ND= 362 NG= 35
FLOPS= 164931. PROFIL= 9580.( 14975.)
RMS= 31.
DECOMPOSITION EXECUTED : SD= 0.55978D+04 HD= 0.55365D+06
IN SEGMENT EXECUT:= NPLAST= 66
RELATIVE OUT OF BALANCE FORCE = 3.820E-07 CHECK = TRUE
STEP 8 TERMINATED, CONVERGENCE AFTER 3 ITERATIONS
TOTAL LOAD FACTOR: LOADING( 1) * 1.000E+00
/DIANA/PO/WR30 19:12:01 34.02-CPU 12.65-IO 7369.-FA BEGIN
TABULA file diana.tb OPENED
/DIANA/PO/WR30 19:12:02 34.40-CPU 12.95-IO 7448.-FA BEGIN
TABULA file diana.tb OPENED
/DIANA/DC/END 19:12:03 34.45-CPU 13.02-IO 7458.-FA STOP
Zauważmy, że w kroku 1 pozostaliśmy w zakresie liniowo-spężystym
czego dowodzą informacje o braku "uplastycznionych" punktów Gaussa
(NPLAST= 0) oraz natychmiastowa zbieżność: Wyniki w postaci tabeli wartości wskazanych w zbiorze non.com wielkości mechanicznych zostały wydrukowane dla każdego przyrostu w zbiorze diana.tb. Poniżej przedstawionie są wyniki dla kroków 1 i 8:
Analysis type NONLIN
Step nr. 1
Load factor 3.000E-01
Result DISPLA TOTAL TRANSL
Axes GLOBAL
Nodnr TDtX TDtY TDtZ X0 Y0 Z0
165 -5.946E-04 1.875E-02 0.000E+00 1.000E+01 1.800E+01 0.000E+00
187 -3.049E-04 1.875E-02 0.000E+00 8.333E+00 1.800E+01 0.000E+00
198 -7.937E-05 1.875E-02 0.000E+00 6.667E+00 1.800E+01 0.000E+00
209 6.328E-05 1.875E-02 0.000E+00 5.000E+00 1.800E+01 0.000E+00
220 1.105E-04 1.875E-02 0.000E+00 3.333E+00 1.800E+01 0.000E+00
231 7.625E-05 1.875E-02 0.000E+00 1.667E+00 1.800E+01 0.000E+00
232 0.000E+00 1.449E-02 0.000E+00 2.971E-16 5.000E+00 0.000E+00
242 0.000E+00 1.875E-02 0.000E+00 1.110E-15 1.800E+01 0.000E+00
Analysis type NONLIN
Step nr. 1
Load factor 3.000E-01
Result FORCE RESIDU TRANSL
Axes GLOBAL
Nodnr FRX FRY FRZ
242 6.482E+00 -5.042E+02 0.000E+00
Analysis type NONLIN
Step nr. 1
Load factor 3.000E-01
Result STRAIN TOTAL GREEN
Axes LOCAL
Location of results INTPNT
Elmnr Intpt Exx Eyy Ezz Gxy X0 Y0 Z0
1 1 -4.855E-04 2.890E-03 -6.010E-04 -1.439E-04 5.153E+00 1.153E-01
2 -4.602E-04 2.784E-03 -5.809E-04 -4.974E-04 5.133E+00 4.253E-01
3 -2.322E-04 2.281E-03 -5.122E-04 -5.458E-05 5.581E+00 1.355E-01
4 -2.431E-04 2.248E-03 -5.013E-04 -2.000E-04 5.563E+00 5.012E-01
Analysis type NONLIN
Step nr. 1
Load factor 3.000E-01
Result STRESS TOTAL CAUCHY
Axes LOCAL
Location of results INTPNT
Elmnr Intpt Sxx Syy Szz Sxy X0 Y0 Z0
1 1 6.737E+00 2.036E+02 0.000E+00 -4.197E+00 5.153E+00 1.153E-01
2 7.043E+00 1.963E+02 0.000E+00 -1.451E+01 5.133E+00 4.253E-01
3 1.633E+01 1.629E+02 0.000E+00 -1.592E+00 5.581E+00 1.355E-01
4 1.506E+01 1.604E+02 0.000E+00 -5.832E+00 5.563E+00 5.012E-01
!!! Pominięto linie !!!
Analysis type NONLIN
Step nr. 8
Load factor 1.000E+00
Result DISPLA TOTAL TRANSL
Axes GLOBAL
Nodnr TDtX TDtY TDtZ X0 Y0 Z0
165 -1.049E-03 6.250E-02 0.000E+00 1.000E+01 1.800E+01 0.000E+00
187 -2.980E-04 6.250E-02 0.000E+00 8.333E+00 1.800E+01 0.000E+00
198 2.613E-04 6.250E-02 0.000E+00 6.667E+00 1.800E+01 0.000E+00
209 5.696E-04 6.250E-02 0.000E+00 5.000E+00 1.800E+01 0.000E+00
220 5.875E-04 6.250E-02 0.000E+00 3.333E+00 1.800E+01 0.000E+00
231 3.577E-04 6.250E-02 0.000E+00 1.667E+00 1.800E+01 0.000E+00
232 0.000E+00 5.333E-02 0.000E+00 2.971E-16 5.000E+00 0.000E+00
242 0.000E+00 6.250E-02 0.000E+00 1.110E-15 1.800E+01 0.000E+00
Analysis type NONLIN
Step nr. 8
Load factor 1.000E+00
Result FORCE RESIDU TRANSL
Axes GLOBAL
Nodnr FRX FRY FRZ
242 1.982E+01 -1.274E+03 0.000E+00
Analysis type NONLIN
Step nr. 8
Load factor 1.000E+00
Result STRAIN TOTAL GREEN
Axes LOCAL
Location of results INTPNT
Elmnr Intpt Exx Eyy Ezz Gxy X0 Y0 Z0
1 1 -1.033E-02 2.469E-02 -1.173E-02 -1.895E-03 5.153E+00 1.153E-01
2 -9.081E-03 2.191E-02 -1.028E-02 -5.571E-03 5.133E+00 4.253E-01
3 -6.539E-03 1.895E-02 -9.647E-03 -9.427E-04 5.581E+00 1.355E-01
4 -6.621E-03 1.852E-02 -9.217E-03 -3.552E-03 5.563E+00 5.012E-01
Analysis type NONLIN
Step nr. 8
Load factor 1.000E+00
Result STRESS TOTAL CAUCHY
Axes LOCAL
Location of results INTPNT
Elmnr Intpt Sxx Syy Szz Sxy X0 Y0 Z0
1 1 1.099E+01 2.956E+02 7.481E-08 -7.437E+00 5.153E+00 1.153E-01
2 1.086E+01 2.870E+02 -6.188E-07 -2.423E+01 5.133E+00 4.253E-01
3 3.097E+01 2.917E+02 -8.557E-08 -4.502E+00 5.581E+00 1.355E-01
4 2.566E+01 2.873E+02 1.031E-07 -1.693E+01 5.563E+00 5.012E-01
Zbiór ten możemy wykorzystać dla utworzenia wykresów zmienności
wybranych wielkości w przestrzeni lub "czasie" (tzn. w kolejnych
krokach przyrostowych w funkcji np. parametru obciążenia).
Najbardziej interesuje nas zawsze nieliniowa zależność przyłożonej
siły od wybranego przemieszczenia, bo pokazuje stan zaawansowania
badanego procesu. Aby narysować taki wykres potrzebujemy
utworzyć plik z dwiema kolumnami liczb, po czym zinterpretować
go dostępnym standardowo programem
gnuplot lub innym narzędziem rysującym (na komputerze
alpha.twins.pk.edu.pl dostępny jest np. wygodny
pakiet xmgr).
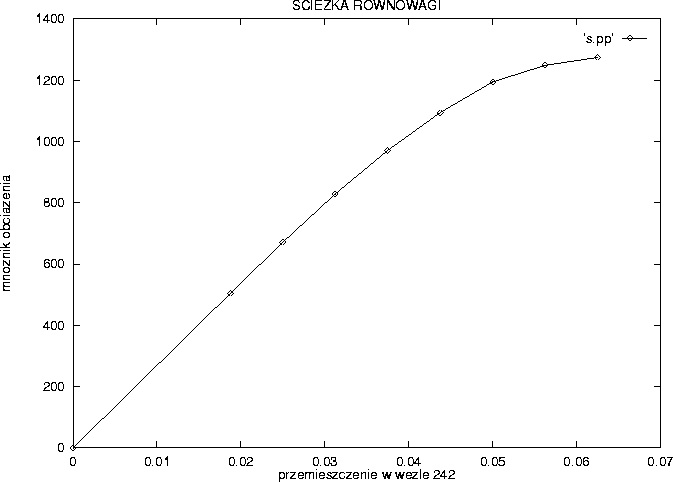
Figure: Ścieżka równowagi dla rozciągania próbki w zakresie
sprężysto-plastycznym
Przykładowy plik sterujący gnuplotem (wywołanie gnuplot nazwa_pliku_sterującego), powodujący wyświetlenie wykresu ze zbioru s.pp na ekranie i stworzenie kopii "postscriptowej" na pliku wykres.ps, wygląda tak:
set data style linespoints set xlabel 'przemieszczenie w wezle 242' set ylabel 'mnoznik obciazenia' set title 'SCIEZKA ROWNOWAGI' plot 's.pp' pause -1 'press enter' set term post set output 'wykres.ps' replot
Plik z danymi do wykresu orzymujemy przez "przeskanowanie" pliku diana.tb, tzn. wybranie z niego tylko informacji o dwóch interesujących nas w danej chwili zmiennych. Najprościej uzyć do tego narzędzia Unixa awk. Przykładowy skrypt wywołujący awk i "skanujący" zbiór diana.tb wygląda tak:
awk 'BEGIN { nn = 0
f = "%15.4e %15.4e\n"
printf f, 0.0, 0.0
}
/DISPLA TOTAL TRANSL/ { nn = 1 }
/FORCE RESIDU TRANSL/ { nn = 2 }
/STRAIN TOTAL GREEN/ { nn = 3 }
/STRESS TOTAL CAUCHY/ { nn = 4 }
{
#
# force vs displacement
#
if (nn == 1 && $1 == 242 ) epsy = $3
if (nn == 2 && $1 == 242 ) { printf f, epsy, -$3 }
#
# stress vs strain
#
#if (nn == 3 && $1 == 1 && $2 == 1 ) epsy = $4
#if (nn == 4 && $1 == 1 && $2 == 1 ) { printf f, epsy, $4 }
}
' < diana.tb > s.pp \rm }
W pliku tym szukamy najpierw określonych nagłówków tabel
(np. DISPLA TOTAL TRANSL) i ustawiamy wskaźniki
(np. nn = 1). Następnie określone pola wybranej linii wydruku
ze wskazanej tabeli są zapamiętywane i drukowane Np. linia 
Figure: Przyrosty przemieszczeń w ostatnim wykonanym kroku
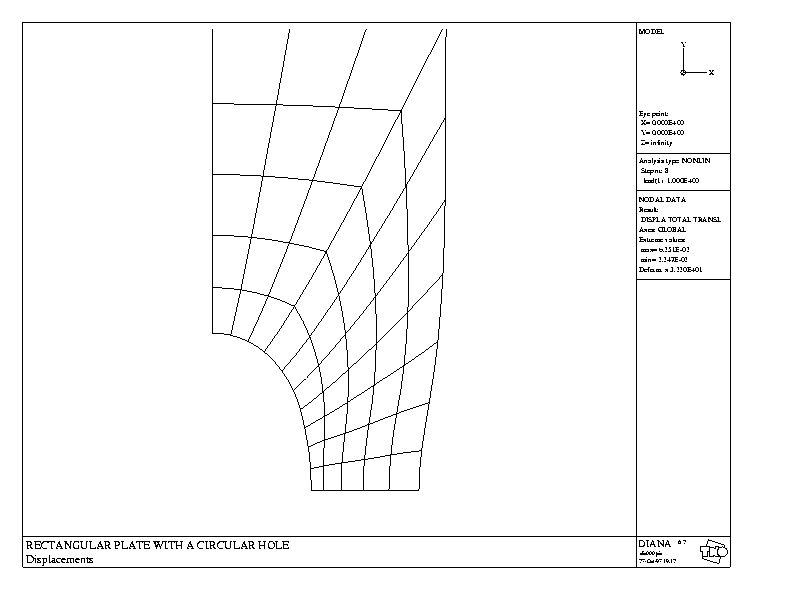
Figure: Całkowite przemieszczenia w zadaniu nieliniowym
Używając powyższych narzędzi otrzymaliśmy ścieżkę równowagi na rys. 6. Na osi pionowej mamy w tym wypadku (ze znakiem przeciwnym) reakcję więzi, którą wymuszamy deformację, czyli połowę siły P rozciągającej próbkę na rys. 2. Oczywiście interesują nas również wyniki w postaci graficznej. Aby uzyskać pliki w formacie GKS, trzeba ponownie uruchomić moduł DIANy *post z odpowiednim zbiorem komend (tu nazwanym graf.com):
*post model : select elemen 1-50 / end model layout charac.h si=10 model li=.. nodes data.d li=- elemen data.f end layout select : elemen 1-50 / : end elemen end select output graphi nonlin fi="din" text "Incremental displacements" displa increm end output output graphi nonlin fi="dis" text "Displacements" displa total end output output graphi nonlin fi="pst" text "Principal plastic strains" strain plasti green princi 1 2 intpnt end output output graphi nonlin fi="stp" text "Principal stresses" stress princi 1 2 intpnt end output *endW tym celu można "odkomentować" kolejną linie w skrypcie run i wysłać zadanie do kolejki.
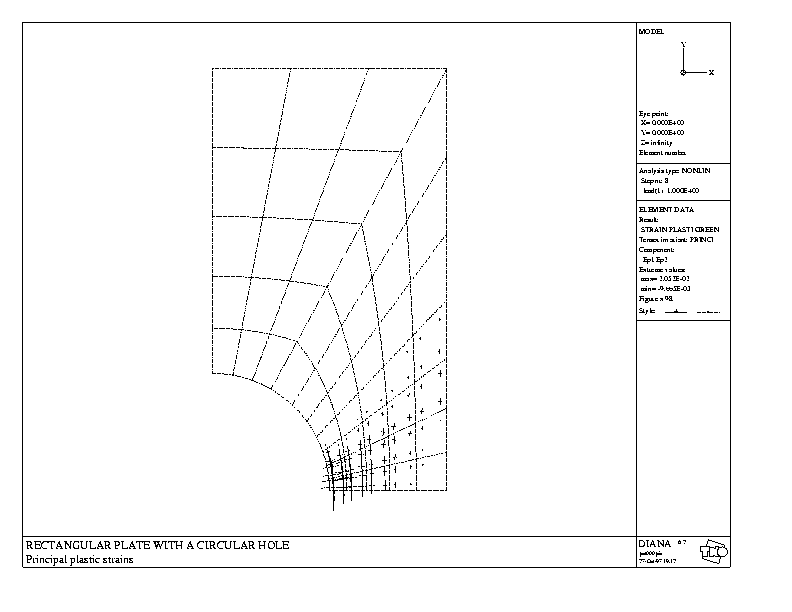
Figure: Główne odkształcenia plastyczne
Figure: Naprężenia główne po ośmiu krokach zadania nieliniowego
W pliku graf.com po zażądaniu zapisania w zbiorze graficznym
informacji o modelu, określeniu formatu rysunku i (opcjonalnym)
wyborze elementów do przedstawienia na rysunku, zlecone
jest wykonanie czterech zbiorów graficznych. Pierwszy stworzony
zbiór din000.pic(rys. 7)
zawiera odpowiednio wyskalowane przyrosty przemieszczeń
z ostatniego kroku procesu przyrostowego (przyrost 8).
Na rys. 7 są one pokazane liniami ciągłymi
razem z wyjściowym, nieodkształconym modelem (linie przerywane).
Drugi zbiór zawiera informacje o całkowitych przemieszczeniach
(rys. 8). Kolejny zbiór pst000.pic zawiera zgodnie z naszym
zaleceniem zawartym w linii:
strain plasti green princi 1 2 intpnt
dane o dwu głównych odkształceniach plastycznych w punktach Gaussa
(rys.9) po zakończeniu przyrostu 8. Linie ciągłe oznaczają
odkształcenia dodatnie (rozciągające), przerywane - ściskające.
Natomiast czwarty zbiór
służy do narysowania naprężeń głównych na rys. 10.
W wypadku wielokrotnego wywoływania DIANy z komendami
graf.com (np. po ponownym przeliczeniu zadania
lub w celu wyboru innych opcji graficznych) będą tworzone
pliki o tych samych nazwach i rozszerzeniach z kolejnymi numerami
(np. pst001.pic).
Warto również czasem skorzystać z postprocesora graficznego FEMVIEW wywoływanego komendą femgvx. Umożliwi to utworzenie zbiorów dla FEMVIEW komendami zawartymi w pliku post.com:
*post select nodes all / elemen all / end elemen end select output femvie nonlin binary fi="plate" displa total strain total princi intpnt coor strain plasti intpnt coor stress total princi intpnt coor end output *endW tym przypadku na zbiorach PLATE.V20 zapisane zostaną informacje o przemieszczeniach, odkształceniach całkowitych i plastycznych oraz napężeniach, które można przy użyciu femgvx obejrzeć w postaci kolorowych map.
Literatura
[1] DIANA Finite Element Analysis,
User's manual , Release 6.1, TNO Building and Construction
Research, Delft (1996).
[2] A. Rajca, Generator siatek TRIANGLE, Prace Instytutu L-5,
Raport nr B-28/97, Politechnika Krakowska (1997).